‘Where did my box go?!’ - Momentarily missed detection in a sequence of frames
The problem
Have you ever tried applying an object detection model on a sequence of frames? if you did, you probably noticed that some of the objects that are detected correctly, are missed in a frame (or frames) and then detected normally again in the following frame\s, as you can see in the following example:
An example of momentarily missed detection of an object. The person riding a bicycle is continuously detected in a sequence of frames but is not detected at the frame in the middle. (taken from [1])
Why does it happen?
There are several well known origins to explain this phenomenon - object can become occluded, blurred or with any other ‘external’ effect that a frame can have in a sequence of frames. let’s call these external factors.
In other cases, like the one in the example above, it is unclear what causes the missed detection.
In recent work called ‘Analysis and a Solution of Momentarily Missed Detection for Anchor-based Object Detectors’ the authors suggest that there is an internal factor in anchor-based object detectors that causes this phenomenon. This factor is explained as an improper behavior of the detectors at the boundaries of anchor boxes. Specifically, when an object moves in the sequence of frames, its predicted score can drop considerably when the optimal anchor for the object switches to it’s neighbor. We will elaborate this point later.
Overall, the authors claim that about 60 to 70% of missed detection cases are caused by external factors, while about 20 to 30% can be explained by the internal factor.
The internal factor
Anchor-based detectors are the most common type of detectors that model the localization of objects as a regression problem. In this approach, default anchor boxes are predefined with several sizes and aspect ratios that are positioned at each grid cell of a feature map. Then the problem is formulated as prediction of offsets to the true bounding box from its closest anchors.
Going back to the internal factor. We can now understand better the meaning of the switch of the optimal anchor for an object to it’s neighbor - when an object moves in a sequence of frames, it can translate to another location, it can appear closer\further from the camera and also appear as if it had turned, that way it’s bounding box might have a different aspect ratio. When that happens, the optimal anchor for the object can switch to another that suits it’s location, size and aspect ratio better. The following example explains these switches visually:
Three types of boundaries between neighboring anchors boxes. (taken from [1])
The authors [1] conducted a simple experiment to single out the internal factor - they generated a sequence of images simulating three types of motion to consider the three types of anchor boundaries shown above: scale, horizontal shift and change in aspect ratio. Then, they passed the sequence as input for SSD detector and plotted the score of two neighbor anchors as a function of the motion factor (scale, shift and aspect ratio change).
At Green-Eye Technology we work with an anchor-based detector and we wanted to check whether our detector suffer from missed detection, so we conducted that experiment as well: Let’s look at horizontal shift - we took the following image and created 61 frames from it by shifting horizontally with values from range [-30, 30]:
We fed our detector with the sequence of frames and noticed that the following bounding box for a weed was momentarily missed between some frames:
We found the relevant anchor responsible for detecting this object and it’s neighbor, and plotted the score in both anchors as a function of the horizontal shift:
You can understand now why the missed detection occurs: between shifts (-6,2) we can see that the score for the object drops below 0.5 and therefore is not taken into account.
The Solution
So far we found out the internal factor that causes this issue - how can we minimize it’s effect?
The authors dig deeper in anchor-based detectors and understood that the internal factor exists because of the way that positive samples are selected. Normally, multiple anchor boxes are selected as positive samples for training if their IOU (intersection over union) with the ground-truth surpasses some threshold (usually 0.5). Since this is a hard threshold, anchors with IOU that is below the threshold, but very very close (0.499), aren’t considered as positive samples for training, which doesn’t really make sense.
They proposed a new method for selecting positive samples: instead of using a hard, binary threshold, lets ‘soften’ it by giving a continuous weight tied with the IOU. The formulation is rather simple:
Weights (Xk and X’k) applied to the loss of anchor k haveing IOU r with the ground-truth box. (taken from [1])
Our ‘modified’ solution
Our case is a little different because we were testing a modification of Yolo v3. Yolo selects one anchor as a positive sample per ground truth box - picks the anchor with the best IOU. In the loss computation during training, predictions with IOU below a certain threshold are ignored. That means that the solution proposed in the paper doesn’t fit exactly, but since the ignored anchors are computed with a binary threshold, maybe soft threshold can help us here as well.
We applied the proposed solution in the following manner:
Let’s look at the confidence loss of Yolo v3:
We realized that if we pick the ignored anchors with a soft threshold instead of a hard threshold, we would allow more relevant (IOU-wise) anchors into the confidence loss, penalizing more false positives and hopefully reaching a better prediction precision.
Results
After training with the same settings, we conducted the experiment from above again and plotted the score as a function of the horizontal shift for the same two anchors from before:
AMAZING! no significant score drop meaning no missed detection!
That’s a great result for our take from the paper. here are some examples from the authors achieved by their solution:
Results reported by [1]. left columns show the missed detection and the score graph as a function of the change before applying the solution and the right columns show the correct detection and the graph after applying the solution.
Summary
Momentarily missed detection is a common issue of anchor-based detectors. The paper we reviewed shed some light regarding the behavior of such detectors around anchor boundaries. Since we always search for ways to improve, we found it exciting to be able to reproduce the paper’s results, while modifying their solution to our needs.
References
[1] Hosoya, Yusuke, Suganuma, Masanori, Okatani, Takayuki. Analysis and a Solution of Momentarily Missed Detection for Anchor-based Object Detectors , arXiv:1910.09212v1 [cs.CV].
Thank you for reading,
Yoav Halevi
Data Scientist @ Greeneye Technology

![An example of momentarily missed detection of an object. The person riding a bicycle is continuously detected in a sequence of frames but is not detected at the frame in the middle. (taken from [1])](https://images.squarespace-cdn.com/content/v1/5decba76ad5fad5d9c5d4eff/1578384068023-XO554W0PRAPN4ZQWPX22/problem_example.JPG)
![Three types of boundaries between neighboring anchors boxes. (taken from [1])](https://images.squarespace-cdn.com/content/v1/5decba76ad5fad5d9c5d4eff/1578384218326-D91FCUOY9113SYECUPMQ/anchor_switch_example.JPG)



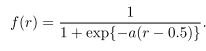
![Weights (Xk and X’k) applied to the loss of anchor k haveing IOU r with the ground-truth box. (taken from [1])](https://images.squarespace-cdn.com/content/v1/5decba76ad5fad5d9c5d4eff/1578392438757-8UV1D8MH53F0QH5EA8RL/soft_sigmoid_graph.JPG)

![Results reported by [1]. left columns show the missed detection and the score graph as a function of the change before applying the solution and the right columns show the correct detection and the graph after applying the solution.](https://images.squarespace-cdn.com/content/v1/5decba76ad5fad5d9c5d4eff/1579019703844-5QZEJ6VUF9G8CSLENKVY/paper_results.PNG)